离散对数

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 1k 阅读时长 ≈ 1 分钟

离散对数(Discretelogarithm,简称DL)是一种基于同余运算和原根的一种对数运算。

基本定义

在群 G 中，g 为 G 的生成元，也就是说群 G 中每一个元素都可以写成 \[y=g^k \]，我们称 k 为 y 在群 G 中的对数，记作 \[k=log_yg \]。 \[ 设 m≥1，(a,m)=1 ，使得 a^d≡1(mod\;m) 成立的最小正整数 d\\ 称为 a 对模 m 的指数或者阶，我们一般将其记为 \delta_m(a) 。 \]

\[ 当 δ_m(a)=φ(m) 时，称 a 是模 m 的原根，简称 m 的原根。 \]

性质

\[ 使得 a ^d ≡ 1 ( mod\; m ) 成立的最小正整数 d ，满足 d ∣ φ ( m ) 。 \]

\[ 模 m 剩余系存在原根的充要条件是 m = 2 , 4 , p^ α , 2 p^ α ，其中 p 为奇素数， α 为正整数。 \]

离散对数问题

爆破

给定\[y≡g^x\;mod\;p\]，不可以暴力枚举x来求解。（误

BSGS

全称是Baby-step giant-step，也叫小步大步法，使用了中间相遇的思想。

令\[x=im+j，其中m=[\sqrt n]\]，i和j都在0到m的范围内

因此\[y=g^x=g^{im+j}\]

变换得\[y(g^{-m})^i=g^j\]

之后我们就可以枚举所所有的j计算，并存在一i个集合S中，然后我们再次枚举i计算\[y(g^{-m})^i\],只要发现计算的结果在S中则说明完成碰撞，得到了i和j。

BSGS是一个时间与空间的折中的方式，我们将一个 \[O(n)\]的时间复杂度，\[O(1)\] 空间复杂度的算法转换为了一个\[O(\sqrt n)\] 的时间复杂度和\[O(\sqrt n)\] 的空间复杂度的算法。

其中

  1. j每次增加表示“baby-step”
  2. i每次增加表示"giant-step"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import gmpy2
def bsgs(g,y,p,bound):
    m=gmpy2.iroot(bound,2)[0]
    S={pow(g,j,p):j for j in range(m)}
    gs=pow(g,-m,p)
    for i in range(m)：
    	if y in S:
            return i*m+S[y]
        y=y * gs %p
        return None
g=
y=
p=
bound=
x=bsgs(g,y,p,bound)

sagemath内置函数：

1
2
#python
bsgs(g,y,bounds,operation)

Pollard‘s Rho algorithm

Pollard’s Rho 算法是一个非常有趣又容易理解的整数因子分解算法，原本用于分解RSA体系中的n，后来又应用于离散对数问题。

加密算法

Elgamal PKC

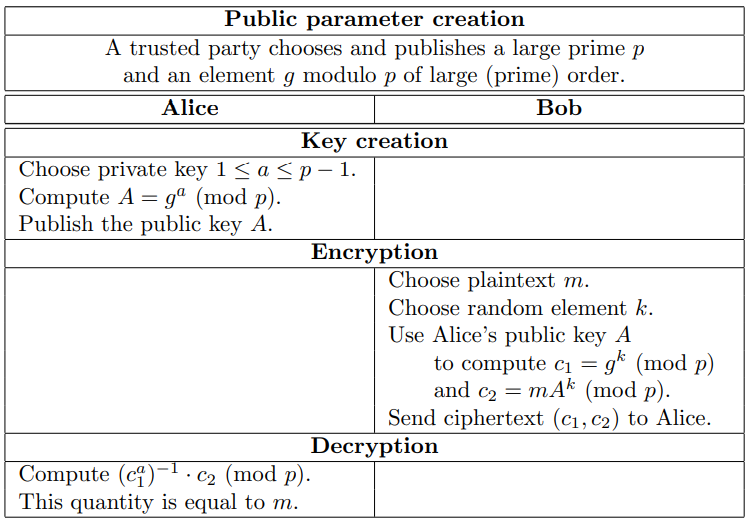
老规矩，Alice传消息给Bob： \[ 公开：大质数p和F^*_p下的生成元g\\ 1.Alice随机选择一个密钥a，计算A=g^a\;mod\;p,并将公钥A传给Bob（g和p其实也是公钥）\\ 2.Bob生成随机数k，计算c_1=g^k\;mod\;p,c_2=mA^k\;mod\;p\\ 3.Alice还原m： (c^a)^{-1}*c_2=(g^{ak})^{-1}*m(A^k)=(g^{ak})^{-1}*mg^{ak}=m\;mod\;p \] image-20210906171507054