PIR
Private Information Retrieval
introduction
Henry Corrigan-Gibbs and Dmitry Kogan二人提出了一个新的PIR方案,使得处理时间变为了对数多项式/次线性级别,并且没有增加开销。
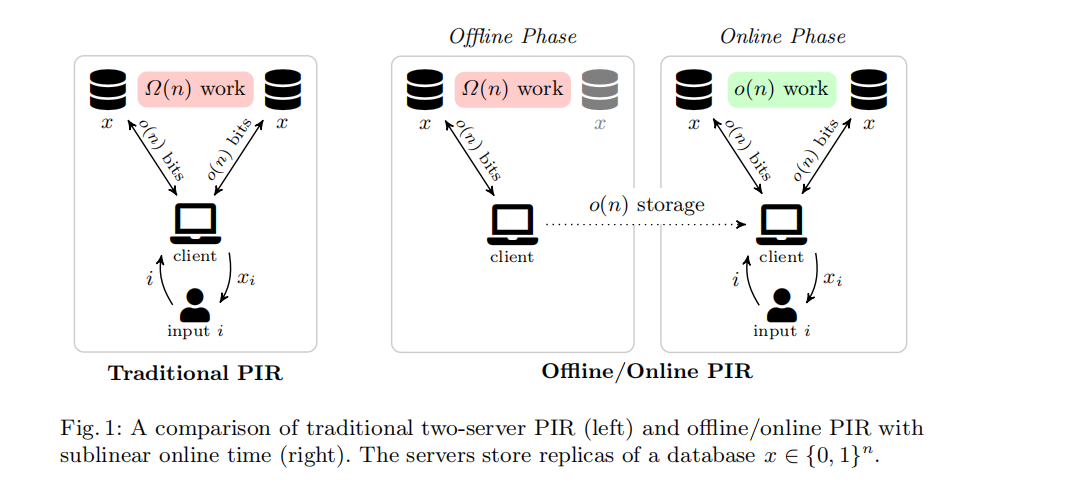
Our idea is to push the (necessary) linear-time server-side computation into a query-independent offlfflffline phase, which allows a subsequent online phase to complete in sublinear time
- In an offline phase, which takes place before the client has decided which bit of the database it wants to retrieve, the client fetches a one-time-use “hint” from the database servers.
- In a subsequent online phase, which takes place after the client has decided which bit of the database it wants to retrieve, the client sends a query to the database servers. Given the servers’ answers to this query, along with the hint prefetched earlier, the client can recover its database bit of interest.
notation
$$ N : the;set ;of ;positive ;integers\
n : the ;set ;{1, 2, . . . , n}\
1^n : 长度为n的全为1的二进制字符\ s-subset of [n] : a;subset;of;size;exactly;s\ \[\begin{pmatrix} [n]\\ s \end{pmatrix}\]:the;set;of;all;s-subsets;of;[n]\ xS: choosing;x;independently;and;uniformly;at; random;from;the;set;S\ xD: choosing;x ∈ S; according ;to ;distribution ;D\ For;p ∈ [0, 1],xBernoulli(p): choosing ;the ;bit ;b ;to; be ;‘1’ ;with ;probability ;p ;and ;‘0’; with ;probability ;1 − p $$
Puncturable pseudorandom sets
非常重要的一个概念
还有术语“puncturable pseudorandom function(puncturable PRF)” and "puncturable pseudorandom set(PRPs)"
PRF key与函数f: [n] -> [n]密切相关 \[ a\;PRF\;key\;punctured \;at \;point\;x^∗ ∈ [n]\; allows \;its \;holder \;to \;evaluate \;f \;at \;every \;point \;in\; [n],\; \\except\; at\; the\;punctured\; point\; x^∗ \] 也就是说punctured key不能对它的持有者揭示任何有关\[f(x^*)\]的信息
同样的, the key for a puncturable pseudorandom set is a compressed representation of a pseudorandom set S ⊆ [n]. The set key punctured at element \[ x^∗ ∈ *S* \]allows its holder to recover all elements of S except the punctured element\[ x^∗ \]. The punctured set key reveals nothing about \[x^∗ \]to its holder, apart from that fact that \[x^∗\] is not one of the remaining elements in S.
Defifinitions
2.1部分介绍了三个重要算法 \[ 设s: N\rightarrow N的函数满足s(n)\leq n.\\ A\;puncturable\; pseudorandom\;set \;with \;set \;size\; s\; consists\; of \;a\; key\; space \;K\\ a \;punctured-key \;space\; K_p\\ \]
下面三个算法:
- \[Gen(1^\lambda,n)\rightarrow sk:传入\lambda 和size n,输出一个set \;key \;sk \in N\]
- \[Punc(sk, i)\rightarrow sk_p:输入sk\in K 和i \in [n],输出一个punctured \;set \; key \;sk_p \in K_p\]
- \[Eval(sk)\rightarrow S:输入key \in K \bigcup K_p, 输出一个集合S \subseteq [n]\]
效率:对任何的安全参数\[ \lambda \in N \],上述三个算法以 \[s(n) * poly(\lambda, log n)\]的时间运行
正确性:对任何\[ \lambda , n \in N\] ,设取样\[sk \leftarrow Gen(1^\lambda, n)\],计算\[S \leftarrow Eval(sk)\],一定有以下:
- \[S \in \begin{pmatrix} [n]\\ s \end{pmatrix}\]
- \[对任意i \in S,Eval(Punc(sk, i)) = S \backslash \{i\}\]
安全性:首先引入Game 1 $$ Game ;1(Puncturable
;pseudorandom ;set ;security).\ For ;,n N, and ;a ;puncturable
;pseudorandom ;set;=(Gen, Punc, Eval)\
定义如下在挑战者和对手之间的游戏:\ -The;challenger;executes;the
;following ;steps:\ \[\begin{align}\
&1.sk \leftarrow Gen(1^\lambda,n)&\\
&2.S \leftarrow Eval(sk)&\\
&3.x^*\stackrel{R}{\longleftarrow}S&\\
&4.sk_p\stackrel{R}{\longleftarrow}Punc(sk, x^*)&\\
并将1^\lambda和sk_p发送给对手。\\
-对手输出一个整数x^{'} \in [n]\\
如果x^{'} = x^*则认为对手获胜
\end{align}\]^*则认为对手获胜 \end{align} $$ 
这里没太看懂。。
Constructions
关于2.2部分,个人的浅薄理解是给出了一些存在性的证明,如下所述。 \[ Fact\;2 \;(Perfectly \;secure \;puncturable \;pseudorandom\; set with\; linear-sized\; keys):\\ 对任何函数s:N \rightarrow N \;with\;s(n) \leqslant n,\;总有一个perfectly \;secure\; puncturable\; pseudorandom \;set \;with \;set \;size \;s\\ 以及,对确定的n来说,the \;set\; keys \;and \;punctured\; keys\;的大小都是(s(n)+O(1))log\;n bits \]
$$ \[\begin{align}\ &Theorem \;3 \;(puncturable\; pseudorandom\; set\; with\; short \;keys \;from\; puncturable\; PRFs):&\\ &\quad假设存在一个\epsilon_F-secure\;puncturable\;PRF,它对于安全的参数\lambda和输入的n, 有长度为\kappa(\lambda,n)的keys和长度为\kappa_p(\lambda,n)&\\ &\quad的punctured\;keys,那么存在一个大小为\Theta(\sqrt{n})的\epsilon-secure \;puncturable \;pseudorandom \;set,对于\lambda和n,有:&\\ &\qquad1.set\; keys\; of\; length\; κ(λ, n) + O(log \;n)\; bits\; and&\\ &\qquad2.punctured\; keys\; of \;length\; κ_p(λ, n) + O(log \;n)\; bits, and&\\ &\qquad3.\epsilon(λ, n) = poly(λ, n) · ( \epsilon_F + 2^{−λ}).&\\ \end{align}\]3.(λ, n) = poly(λ, n) · ( _F + 2^{−λ}).&\ \end{align} $$
然后构造了一个puncturable pseudorandom set来证明上述Theorem: $$ Construction;4 ;(Puncturable; pseudorandom ;set ;from ;puncturable ;PRF).\ Given; a ;puncturable; PRF ;F = (PRFGen, PRFPunc, PRFEval),\ we; construct ;a ;puncturable ;pseudorandom; set ;_F = (Gen, Punc, Eval);with; set ;size; s(n) ;:= \ \[\begin{align}\ &\psi_F.Gen(1^\lambda, n) \rightarrow sk& \\ &\quad-重复以下最多\lambda次:&\\ &\qquad ·k \leftarrow PRFGen(1^\lambda, n).&\\ &\qquad ·计算S \leftarrow {PRFEval(k,1),PRFEval(k,2),···,PRFEval(k,s(n))}&\\ &\qquad ·如果|S| = s(n),停止并输出sk \leftarrow(n,k).输出⊥(这里没懂,输出垂直?)&\\ &\quad-在运行\lambda次后循环不成功,输出⊥&\\\\ &\psi_F.Punc(sk,i) \rightarrow sk_p& \\ &\quad-将密钥解析成(n, k).&\\ &\quad-找到最小的l满足PRFEval(k,l)=i.&\\ &\qquad\;如果不存在这样的l,输出⊥&\\ &\quad-计算k_p \leftarrow PRFPunc(k,l),并输出sk_p \leftarrow (n,k_p).&\\\\ &\psi_F.Eval(sk) \rightarrow S& \\ &\quad-将密钥解析成(n,k).&\\ &\quad-输出集合S \leftarrow {PRFEval(k,1),PRFEval(k,2),···,PRFEval(k,s(n))}.&\\ &\quad-(If \;k\; is\; punctured \;at\; some \;value, \;skip\; this \;value\; when\; computing\; S).&\\ \end{align}\](If ;k; is; punctured ;at; some ;value, ;skip; this ;value; when; computing; S).&\ \end{align} \[ 注意:Gen失败的概率很小,但不代表不会失败,我们可以让sk=⊥是某些固定的集合(例如[s])来保证上述theorem完全正确。 \] Corollary;6. ;Assuming; that ;pseudorandom ;generators; (PRGs); exist,\ there ;exists; ;a ;secure ;puncturable; pseudorandom ;set; with ;set ;size; Θ() $$ theorem 7引入了一个fast membership testing的概念,涉及到一个InSet函数,运行速度是poly的,其实就是判断i是否在PRPs.Eval(sk)中,不展开写了。
Shifting puncturable pseudorandom sets
引入了两个PRPs的性质: \[ \begin{align*} &1.GenWith(1^\lambda,n,i) \rightarrow sk,\;输出的sk满足i\in Eval(sk)&\\ &2.Shift(sk, \delta) \rightarrow sk^{'},即输出的sk^{'}满足Eval(sk^{'}) = {i+\delta\;|\;i \in Eval(sk)},对Eval的结果做了一个shift& \end{align*} \]
不失一般性,可以假设任何PRs都有这两条性质
Two-server PIR with sublinear online time
Defifinition
分为这五步: \[ \begin{align}\ &1.client使用Setup算法生成密钥ck和hint\;q_h,发送q_h给offline\;server。注意Setup算法可提前运行。 &\\ &2.offline\;server接收到q_h后运行Hint算法,生成hint\;h并发给clinet。 &\\ &3.client决定index\;i后,传ck和i给Query算法,生成query\;q并发给online\;server。 &\\ &4.online\;server传q给Answer算法,算出a返回给client。 &\\ &5.client传h和a到Reconstruct算法,输出数据库的第i个比特。 &\\ \end{align} \] 综上,offline/online PIR scheme是五个算法(Setup, Hint, Query, Answer, Reconstruct)组成的五元组: \[ \begin{align}\ &Setup(1^\lambda,n) \rightarrow(ck, q_h),\lambda是安全的参数 &\\ &Hint(x,q_h) \rightarrow h,x是数据库中的n个数据 &\\ &Query(ck,i) \rightarrow q &\\ &Answer^x(q) \rightarrow a &\\ &Reconstruct(h,a) \rightarrow x_i &\\ \end{align} \]
New constructions
基本上是从原始PIR到计算安全的PIR再到加入可穿刺的伪随机集的PIR版本
下图给了运行效率的上界,后面也说了如果只考虑计算安全(舍弃数据统计安全)就能降低开销。

Two-server computational offlfflffline/online PIR:

引入puncturable pseudorandom sets后,PIR的效率可进一步提高:

Construction 16 (Two-server PIR with sublinear online time)
\[ \begin{align} &还是那些配置:s:N \rightarrow N ,\psi = (Gen, Punc, Eval)\;with\;key\;space K,punctured-key\;space\; K_p,&\\ &extended\;by\;routines(Shift,GenWith),\;Throughout, let\;m := (n/s(n))log\;n. &\\ &Offline\;phase: &\\ &\quad Setup(1^\lambda,n) \rightarrow ck,q_h: &\\ &\qquad sk \leftarrow Gen(1^\lambda,n) &\\ &\qquad sample\;\delta_1,...,\delta_m \stackrel{R}{\longleftarrow}[n]&\\ &\qquad ck \leftarrow (sk,\delta_1,...,\delta_m)&\\ &\qquad output\;ck\;and\;q_h \leftarrow sk&\\\\ &\quad Hint(q_h,x \in \{0,1\}^n)\rightarrow h \in \{0,1\}^m &\\ &\qquad parse\;q_h\;as\;sk \in K\;and\;\delta\in [n]^m &\\ &\qquad for\;j=1,...,m\;do:&\\ &\qquad\quad S_j \leftarrow Eval(Shift(sk,\delta_j))&\\ &\qquad\quad h_j \leftarrow \sum_{i\in S_j}x_i\;mod\;2&\\ &\qquad output\;h \leftarrow(h_1,...,h_m)&\\\\ &Online\; phase &\\ &\quad Query(ck, i\in [n]) \rightarrow q\in K_p&\\ &\qquad parse\;ck\;as\;sk\in K\;and\;\delta\in[n]^m&\\ &\qquad sample\;a\;bit\;b\stackrel{R}{\longleftarrow}Bernouli(\frac{s-1}{n})&\\ &\qquad find\;a\;j\in[m]\;s.t.\;i-\delta_j \in Eval(sk)&\\ &\qquad if\;such\;a\;j\in[m]\;exists:&\\ &\qquad\quad sk_q \leftarrow Shift(sk,\delta_j)&\\ &\qquad otherwise:&\\ &\qquad\quad j \leftarrow ⊥&\\ &\qquad\quad i^{'} \stackrel{R}{\longleftarrow} Eval(sk)&\\ &\qquad\quad sk_q \leftarrow Shift(sk, i-i^{'})&\\ &\qquad if\;b=0:\qquad i_{punc} \leftarrow i&\\ &\qquad else: \qquad\quad\;\;\; i_{punc} \stackrel{R}{\longleftarrow} Eval(sk_q)\backslash \{i\}&\\ &\qquad output\;q \leftarrow Punc(sk_q, i_{punc}) &\\\\ &\quad Answer^x(q\in K_p )\rightarrow a\in\{0,1\}&\\ &\qquad S \leftarrow Eval(q)&\\ &\qquad return a \leftarrow \sum_{i\in S}x_i\;mod\;2&\\\\ &\quad Reconstruct(h\in \{0,1\}^m,a\in \{0,1\}) \rightarrow x_i &\\ &\qquad let\;j \;and\;b\;be\;as\;in\;Query&\\ &\qquad if\;j=⊥\;or\;b=0\;then\;output\;⊥ &\\ &\qquad output\;x_i\leftarrow h_j-a\;mod\;2 &\\ \end{align} \]
读paper的总结:
Private Information Retrievalwith Sublinear Online Time
第一篇,是Henry Corrigan-Gibbs和Dmitry Kogan二人写的,将PIR的过程拆成离线和在线阶段,并puncturable pseudorandom sets(后写为PRS)的概念引入其中,线性的计算放到离线阶段,使在线阶段的计算只有次线性的,而且没有引入额外的存储(其实我觉得是有的,毕竟client生成n(1/2)个同样大小的sets,还是生成了n的存储量,并且这些sets都要发给离线服务器算出hint,使得离线阶段的传输量是n;但是在在线阶段确实不需要更多的存储了,传输带宽也只是n(1/2)大小的)
总的来说,关键点是可穿刺的伪随机集,它能去掉某一点的信息,并且在客户端能恢复该点。原始的PRS有三个功能函数,(Genn(1^λ , n), Punc(sk, i), Eval(sk, i)),通过输入安全参数λ和数据库大小n,Gen函数生成一个密钥,Punc函数进行穿刺,Eval函数密钥sk变成集合S;后面还加了两个功能函数GenWith(1^λ , n, i)和Shift(sk, δ),GenWith用于生成有指定元素的密钥,Shift就和它函数名一样,对密钥在有限域下进行一个加操作。
之后就是用前面所提出的PRS融入到PIR方案中,大致的流程如下:
- client在随机的概率分布下生成n(1/2)个大小为n(1/2)的集合S,全部发给离线计算服务器计算异或值返回给client
- 找一个存在x的集合S_i,对其进行穿刺(可以当作找到并丢弃x),然后发给在线服务器,返回去掉x的异或值
- 把1和2的结果进行异或,即可抵消其他的值,只留下x。由于两个服务器是不可进行交流的,因此可以两个服务器无法获取有关x的信息。
- 如果要进行多次取值,那就多了一个人refresh操作更新密钥,即将刚刚用过的S更新否则再次使用会被发现。具体方法是在2同时生成一个集合S‘,对其进行x的穿刺然后发给离线服务器,再得到S’的异或值,拿到后将这个异或值与x异或就可以得到S‘的hint
后面还介绍了单服务器的情况,因为离线在线阶段在一个服务器上了,所以不能直接发集合过去,否则也会被发现。文中引入了全同态加密来描述,利用全同态方案对S进行加密再发给服务器,之后的步骤和上述差不多。
Efficient Transformation Capabilities of Single Database Private Block Retrieval
这一篇的思路和第一篇就很不一样了,没有采用离线/在线服务器的模式,也没有使用穿刺伪随机集,他基于一个NP问题即二次剩余构造单项陷门函数,和rabin系统类似,因此可以一次性获得一个block的数据(该文中把数据库当成u*v的矩阵数据,一次可以获得某一行的数据)。
在这篇里面学到了两个概念,Information-theoretic PIR和Computationally bounded PIR ,第一篇虽然没有介绍但是也用到了,当时就没看懂。信息论的PIR指存在多个服务器,它们享有同一个数据库的copy但相互之间不进行沟通;计算有界的PIR是指基于某个密码假设的PIR方案。
这篇的实现就是利用加科比符号和二次剩余,具体就不展开了了,对我们要的研究方向不太一样。而且它的运算时间是线性的哈哈哈,还不如第一篇,我记得是复杂度u*v加一个log,那对于数据库大小来说就是线性的。不过他有一个优点是构造的方案可以在信息论PIR和计算有界PIR之间互相转换,这是其他方案难以做到的。
Puncturable Pseudorandom Sets and Private Information Retrieval with Near-Optimal Online Bandwidth and Time
这一篇是在第一篇的基础上发展过来的,与第一篇相比,他的优点是在不增加计算时间的基础上减少了传输阶段所用的带宽:离线阶段仅传输n(1/2)大小的消息至left服务器,client收到一个n(1/2)大小的hint,在线阶段的带宽仅为O(1),先前的O(n^(1/2))。但他采用了一种弱化PRS的方案,也即更通用的PRS,所以不像第一篇那样,这一篇存在不可忽略的概率导致结果出错,但总的来说正确率仍然保持的较高(单次2/3的正确率,并行运行128次),可是在第一篇中对x进行穿刺时仍然可能输出一个错误结果’⊥‘,所以我认为这个错误不是什么大问题。
既然达到了不同的效果,那么这一篇所用的Privately Puncturable PRFs肯定与前面的不同,更一般化的 Generalized Privately Puncturable Pseudorandom Set如下:(Gen(1^λ , n), Set(sk), Member(sk, x), Puncture(msk, x)), 多了一个member函数用于测试x是否在sk生成的集合中,同时Gen函数不仅会生成密钥sk,还会生成主密钥msk,这个也是降低传输带宽的关键点。
至于实现过程,其实和第一篇大同小异,仍然是利用集合的异或来恢复x,这里面多加了个超时机制(我是这么理解的),当超时时就会返回一个默认的异或值0,这也是出错的由来。至于refresh阶段也和第一篇类似。
Batched Differentially Private Information Retrieval
这一篇也没有用穿刺伪随机集,他保留了离线在线分离的计算,自己设计了一个新的方法: differentially private-PIR(DPPIR)。最终的效果是把两次的运算时间变成了O(n^(1/2)+constant*n),传输带宽是O(1),带宽都降了不少但运算时间就变成了线性的。
看后面似乎运行条件也比较苛刻,需要同时多个用户查询,批处理查询才能实现这个效率,对主线帮助不大就不细看了。
Private Blocklist Lookups with Checklist
这一篇又是CK20两人的paper,个人感觉不是纯理论上的,而是偏应用层面了。大概就是运用PIR方案实现对服务器端的字符串匹配,判断client处的字符串是否在服务器中,并且不泄露字符串的信息,优点还有不需要存储整个blocklist(类似于第二篇,将服务器端的数据库看作是一个矩阵,每次匹配的是某一行的字符)。还能使得服务端的计算是次线性的,最关键的是——它在blocklist经常更新的时候也满足,与我们的需求类似,值得好好研读;除此之外还有一些在运算速度上的提升等等。
PRS的构造和第一篇的类似,是(Gen, GenWith, Eval, Punc),实现过程和第一篇有很大不同了。
大致的流程还是和第一篇类似,不过是从伯努利概型中根据(2(n^(1/2)-1)/n)的概率中生成β,在生成query查询时搞了两个方案,每个方案都有两套punctured pseudorandom secret key,根据β的值选择某一方案生成查询q,发给right后和第一篇是一样的,返回的answer a也均可以完成对D_i的重构。
至于为什么能满足数据可更新,我目前粗浅的理解只是把数据不断分为更小的块,每次更新都使得较大的那一块保持不变而只有小块改变,因此left服务器对hint的更新不至于是O(n^(1/2))以上的。