Zero Knowledge Proofs
This is the record of my study of ZKP
latex是真难敲这些密码学定义，干脆截图
Introduction and History of ZKP
what is Proofs
Mainly to introduce some definitions：
Proofs: For a Claim, the Prover provides a proof w to prove the correctness of the Claim x, and the Verifier decides to accept/reject based on the proof
\[ \begin{align*}\label{2} & \rm \textbf{Def: A language }\textit{L} \text{ is a set of binary strings x}\\ \end{align*}\]
For example: Large number factoring(N = p*q), quadratic residue(y, N), the two graphs are isomorphic.
Zero Knowledge Proofs means Prover prove that I could prove it If I felt like it.
Zero Knowledge Interactive Proofs
there are Two New Ingredients: Interactive and Probabilistic Proofs:
- Interaction: rather than passively “reading” proof, verifier engages in a non-trivial interaction with the prover.
- Randomness: verifier is randomized (tosses coins as a primitive operation), and can err in accept/reject with small probability
- PS: the prover can compute in unbounded time, but the verifier can just compute in Polynominal-time(PPT)
e.g., the prover proves to the color-blind verifier that a flag has two colors, the verifier flips a coin to decide whether to flip the flag, and the prover guesses the result of the coin based on the flags' obverse and reverse. And if we repeat the progress k times, the $ prob_{coins}((1/2)^k$
Define Interactive Proofs
\[
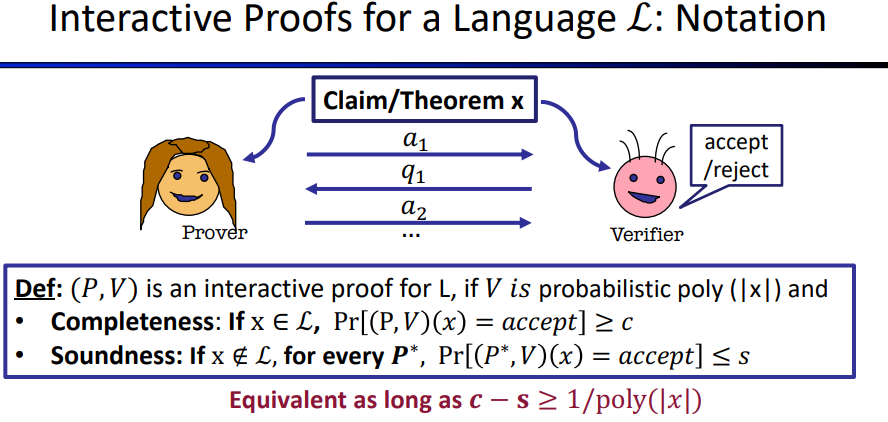\begin{align*}\label{eq1}
& \text{completeness means if x} \in L,\;V\text{ always accepts}\\
& \text{soundness means if x} \notin L,\; \text{for all }
\textcolor[rgb]{0,0,1}{cheating \;prover\;strategy},V \text{ will not
accept except with negligible probability. }
\end{align*}
\] so class of languages IP = {L for which there is an
interactive proof}
What is zero-knowledge
For true Statements, What the verifier can compute after the interaction = What the verifier could have computed before interaction
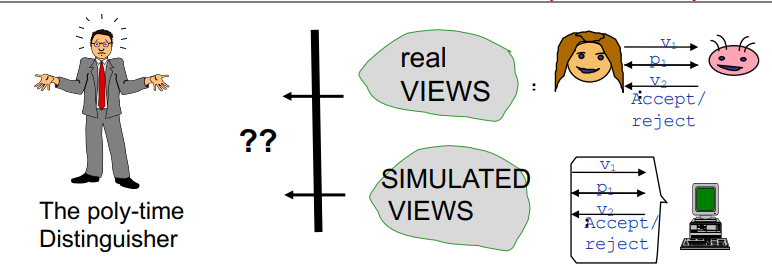
Now we introduce the concept of simulation paradigm
The Simulation Paradigm
V’s view gives him nothing new, if he could have simulated it its own
s.t simulated view and real-view are
computationally-Indistinguishable
Working through a Simulation for QR Protocol: \[ \begin{align} & view_V(P,V):\\ & Transcript = (s, b, z)\\ & Coins = b \end{align} \] so the output of simulation should be (s, b, z)
Computational Indistinguishability
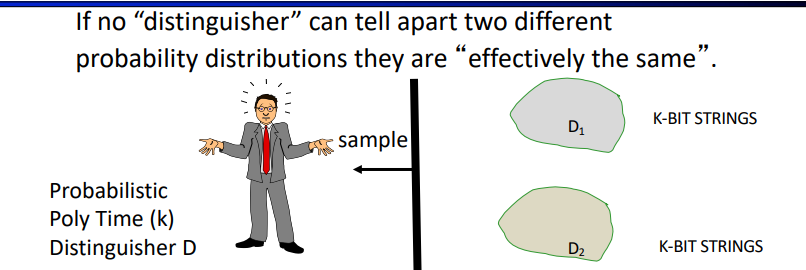
For all distinguisher algorithms D, even after receiving a polynomial number of samples from \(D_b, \text{Prob[D guesses b] <1/2 + negl(k)}\)
Zero Knowledge: Definition
An Interactive Protocol (P,V) is zero-knowledge for a language \(L\) if there exists a \(\textcolor[rgb]{0,0,1}{PPT}\) algorithm Sim (a simulator) such that $ L,$ the following two probability distributions are \(\textcolor[rgb]{0,0,1}{poly-time}\) indistinguishable:
- \(View_V(P,V)[x] = {(q_1,a_1,q_2,a_2,…,coins\;of\; V)}\)
- \(Sim(x, 1^{\lambda}),\lambda\text{- security parameter allows sufficient Runtime onn small x}\)
and we can get the define: (P,V) is a zero-knowledge interactive protocol if it is complete, sound and zero-knowledge.
but what if V is not honest? we need a further definition:
also, there are several types of ZK:
- Computationally indistinguishable distributions = CZK
- Perfectly identical distributions = PZK
- Statistically close distributions = SZK
ZK proof of Knowledge
it seems prover can not only prove the claim x(e.g. y is the quadratic residual under mode N), but also she knows more(the square root of y mod N), so we need extractor to get the knowledge.
the concept of ZKPOK is as follows:
Miscellaneous
do all NP Languages have Zero Knowledge Interactive Proofs?
the answer is yes!
Theorem[GMW86,Naor]: If one-way functions exist, then every L in NP has computational zero knowledge interactive proofs
the ideas of the proof:
- [GMW87] Showed ZK interactive proof for G3-COLOR
using bit- commitments
- for any L in NP, \(L <_p \text{G3-COLOR}\)(due to NPC reducibility)
- every instance x can be reduced to graph \(G_x\) such that:
- if x in L the \(G_x\) is 3 colorable; if not, \(G_x\) is not 3 colorable
- [Naor] showed if One Way Function exits, then bit commitment protocol exits.
Bit Commitment Protocol
i think it's a kind of variant of signature?
CZK examples
quiz
Overview of Modern SNARK Constructions
this class is focusing on None-Interactive Proof
What is a SNARK?
review arithmetic circuits
arithmetic circuits: \(C: \text{F}^n \rightarrow \text{F and |C| = # gates in }C\)
categories
- An unstructured circuit: a circuit with arbitrary wires
- A structured circuit:
M is often called a virtual machine (VM) -- one step of a processor
(preprocessing) NARK: Non-interactive ARgument of Knowledge
Definition: $$ \[\begin{align*}\label{lab3}
& Premilinary:\\
& \text{public arithmetic circuit: }C(x,w) \rightarrow
\text{F},\text{where } x\text{ is the statement in }F^n, \text{and
}w\text{ is the secret witness in }F^m\\
& \text{Preprocessing(setup): S(}C\text{)}\rightarrow \text{public
parameters }(pp, vp)\\
& \text{so a preprocessing NARK is a triple }(S,P,V):\\
& \bullet\text{S(C)} \rightarrow \text{public parameters (pp, vp)
for prover and verifier}\\
& \bullet\text{P(pp, x, w)} \rightarrow \text{proof }\pi\\
& \bullet\text{V(vp, x, }\pi \text{)} \rightarrow \text{accept or
reject}
\end{align*}\] $$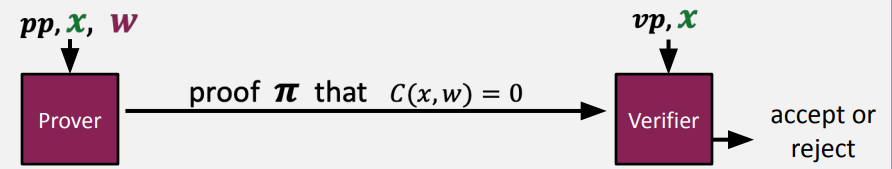 
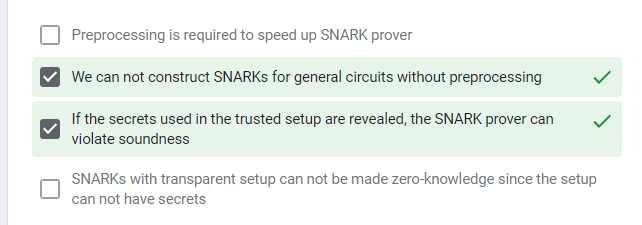
requirements (informal)
Types of preprocessing Setup
Setup for circuit C: \(S(C, r) \rightarrow \text{public parameters }(pp, vp)\) where r is a random bit
- trusted setup per circuit: S(C, r) random r must be kept secret from prover
- trusted but universal (updatable) setup: secret r is independt of C
- $ S = (S_{init}, S_{index})$
- \(S_{init}(\lambda;r)\rightarrow \text{gp, which is one-time setup by secret r}\)
- \(S_{index}(gp,C)\rightarrow(pp, vp), \text{which is used many times}\)
- transparent setup: S(C) does not use secret data(or trusted setup)
for example:
knowledge soundness
\(\text{how can we know P "know" w?} \rightarrow \text{P knows w, if w can be extracted from P}\)
I think the A here is to consider all P (honest d + malicious)
SNARK: a Succinct ARgument of Knowledge
a succinct proprocessing NARK is a triple(S, P, V) balabala(see above)
- need a short proof (len(\(\pi\))=sublinear(|w|))
- fast to verify (time(V)=\(O_\lambda(|x|, sublinear(|C|))\)) (allowing verifier sufficient time to know x but cant learn all of C, so vp is a short summary of circuit)
so SNARK is a NARK(with complete and knowledge sound) that is succinct.
zk-SNARK is a SNARK that is also zero knowledge
Building an efficient SNARK
we just need two steps to get a SNARK for general circuits, combining:
- A functional commitment scheme (Cryptographic object)
- A compatible interactive oracle proof(IOP, which is information theoretic object)
Commitments
two algorithms:
- \(commit(m,r)\rightarrow com \;\;\;\;\;\text{(r chosen at random)}\)
- \(verify(m,com,r)\rightarrow \text{accept or reject}\)
Properties: (informal)
- binding: \(\rightarrow \text{a malicious committer cant produce a commitment and there is no two valid openings for com}\)
- hiding: \(\rightarrow \text{com reveals nothing about committed data}\)
for example:
use Hash function as commitment
Committing to a function
next picture shows how to committe to a function:
the definition of committing to a function:
Four important functional commitments
equality test protocol
there is a useful observation: \[ \begin{align} & \text{for a }f\in F_{p}^{(\leq d)}[X],\text{ and } r \stackrel{$}{\leftarrow}F_p: Pr[f(r) = 0] \leq d/p \;(*)\\ & \text{suppose p} \approx2^{256} \text{and d} \leq 2^{40},\text{the d/p is negligible}\\ & \text{so for }r \stackrel{$}{\leftarrow}F_p: \text{ if f(r)=0 then f is identically zero w.h.p}\\ & \text{this is a simple zere test for a committed polynomial} \end{align} \] further， SZDL lemma: (*) also holds for multivariate polynomials (where d is total degree of f)
now we can get this:
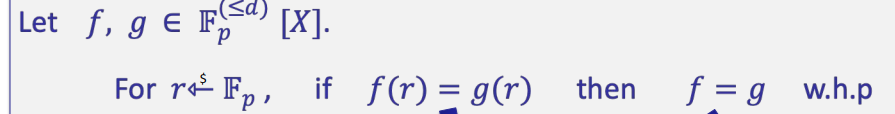
which is a simple equality test for two committed polynomials.
so the equalitty test protocol is:
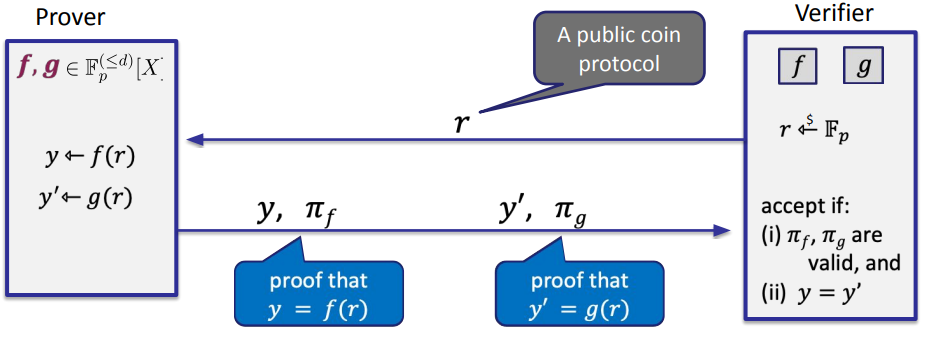
but this is interactive, we want none-interactive to make it a SNARK, the Fiat-Shamir transform can do it.
The Fiat-Shamir transform: \(H:M\rightarrow R \text{ a cryptographic hash function}\), the idea: prover generates verifier's random bits on its own using H
H is also modeled as a Random Oracle (RO)
now we can get a SNARK for polynomial equality testing (just let the r generated by H)
\(F-IOP\) (Poly IOP)
Goal: make a functional commitment to a SNARK for general circuits
example :
Here's how F-IOP works:
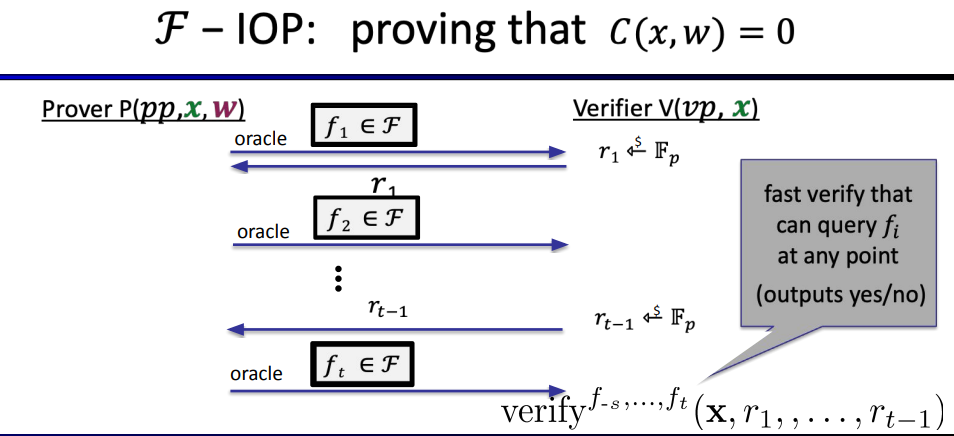
properties:
- Complete: \(if \; \exists w:C(x,w)=0 \text{ then Pr[verifier accepts]=1}\)
- (Unconditional) knowledge sound (as an IOP): [\(\text{extractor is given }(x, f_1,r_1,...,r_{t-1}, f_t) \text{ and outputs w}\)]
- Optional: Zero knowledge (for a zk-SNARK)
example:
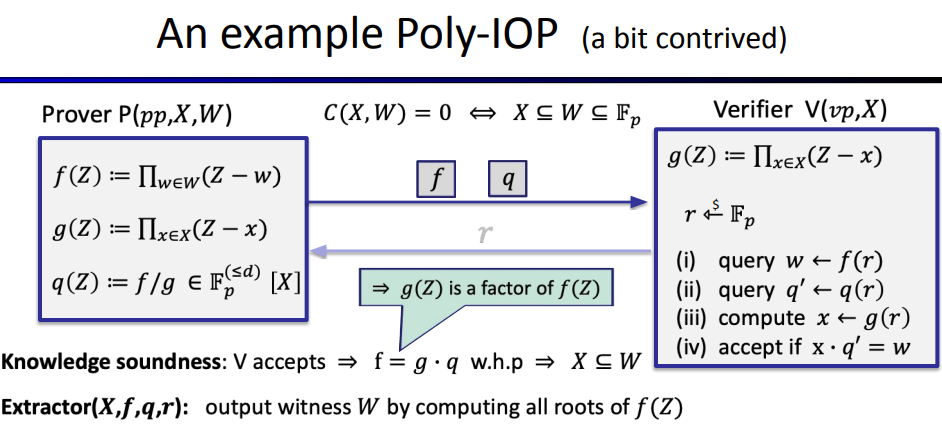
although this process is interactive, we can use Fiat-Sharmir transformer to turn it to an none-interactive process(SNARK)
Miscellaneous
question
- In the Poly-IOP example listed above, sending the commitment of f and q to the verifier is what is done. According to the definition of commitment, there needs to be f and random r to open and verify, but apparently the verifier does not have this data (This problem also exists in other examples) (this problem may be because I do not know about commitment)
quiz
Libraries and Compilers to build ZKP
introducting how to instance a zkp
ZKP Programmability
something about \(\phi\):
- in theory, witness w can be a factorization of integer x, is the sk for pk x
- in practice, \(\phi\) is an "arithmetic circuit", over inputs x and w.
AC as circuit has inputs, gates and wires
R1CS: format for ZKP ACs
- x: field elements \(x_1, ...x_l\)
- w: \(w_1, ...w_{m-l-1}\)
- \(\phi\): n equations of form:
- \(\alpha \times\beta=\gamma\)
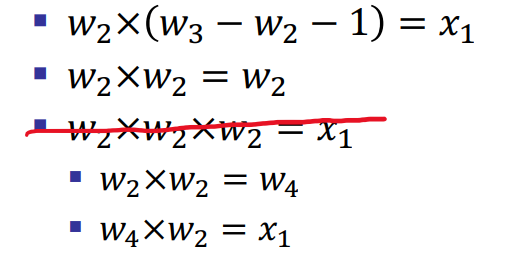
The definition of the extension is matrix-based, but we can treat each of these row vectors as a linear R1CS:
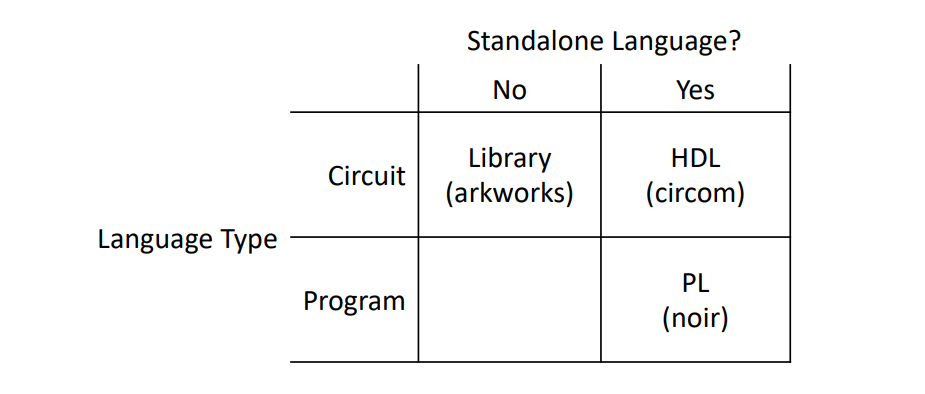
The next step is to build R1CS from three parts: HDL, Library, Compiler, using examples that are all Sudoku
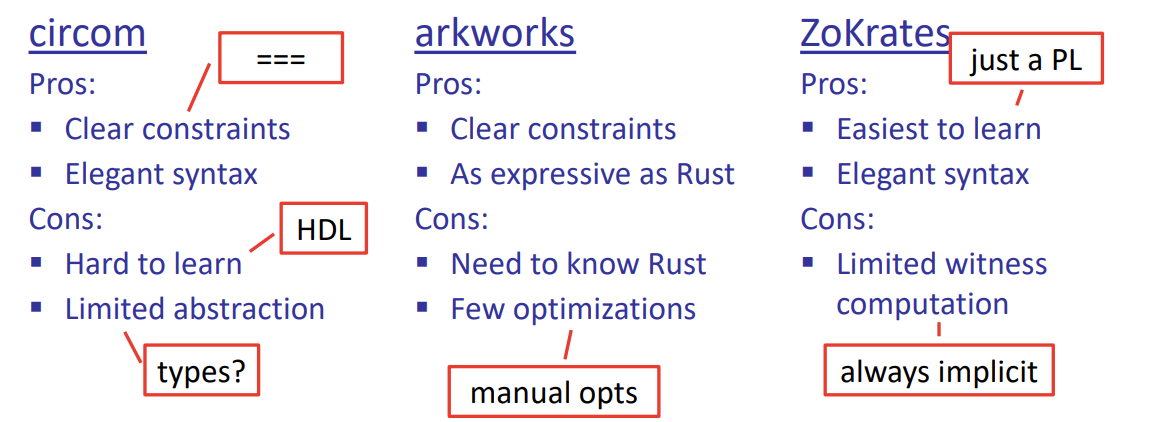
HDL(use Circom)
PL VS HDL:
Circom does:
https://docs.circom.io/
there are several basic method in the code, like judging two nums not equal, num in range of 4bits, and advanced applications.
code: https://github.com/rdi-berkeley/zkp-course-lecture3-code/blob/main/circom/sudoku.circom
library(use arkwork)
so we can just use this library in some certain pl, just using their syntax.
https://github.com/arkworks-rs/r1cs-tutorial/
code: https://github.com/rdi-berkeley/zkp-course-lecture3-code/tree/main/arkworks
compiler(use ZoKrates)
the idea of this way is using variables, functions, and arrays in the circuit.
but there is no way to compute witness(?), all witness must be provided as input.
code:https://github.com/rdi-berkeley/zkp-course-lecture3-code/blob/main/zokrates/root.zok
An overview of prominent ZKP toolchains
comparison:
other tools:
Misc
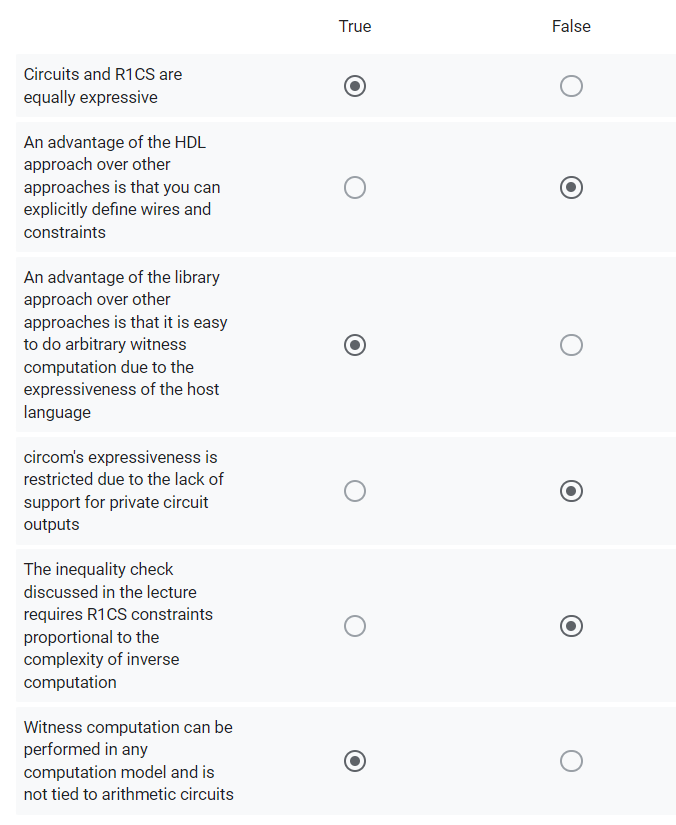
quiz:
Interactive Proofs
Introducing ip and checksum protocols
Plonk Interactive Oracle Proofs (IOP)
introducing widely used SNARK called Plonk, understanding all the component that make up the SNARK.