ECC
抄点ECC笔记
ECC
定义:ECC 全称为椭圆曲线加密,EllipseCurve Cryptography,是一种基于椭圆曲线数学的公钥密码。与传统的基于大质数因子分解困难性的加密方法不同,ECC 依赖于解决椭圆曲线离散对数问题的困难性。它的优势主要在于相对于其它方法,它可以在使用较短密钥长度的同时保持相同的密码强度。目前椭圆曲线主要采用的有限域有:
- 以素数为模的整数域 GF(p),通常在通用处理器上更为有效。
- 特征为 2 的伽罗华域 GF(2^m),可以设计专门的硬件。
(from CTF Wiki)
基础
定义式:\[y^2+axy+by=x^3+cx^2+dx+e\],其中的所有系数都是在某个有限域GF(p)中的元素,p是一个大素数;
最常用的方程为:\[y^2=x^3+ax+b\],需要满足条件\[4a^3+27b^2\;mod\; p \neq 0\]
该定义要求曲线是非奇异的,意味着曲线不会自我相交或没有顶点。
群操作
假设用加法符号“+”表示它的群操作,事实上,E(Fp)对于运算+构成一个阿贝尔群(交换群,满足逆元存在,封闭性等),存在无穷远点O
逆元
定义群元素P的逆元-P,则P+(-P)=O \[ 若P=(x_p,y_p)\;\;\; 则-P=(x_p,p-y_p) \]
数乘
\[ 定义Q=kP,可以看作k个P相加得到Q \\ 若O=tP,则称P的阶是t \]
相异点相加
\[P(x_1,y_1),Q(x_2,y_2),R(x_3,y_3)\;\;P+Q=R\]
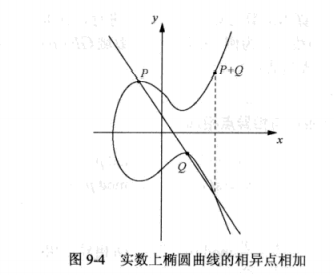 \[
x_3=(\frac{y_2-y_1}{x_2-x_1})^2-x_1-x_2\;mod\;p\\
y_3=\frac{y_2-y_1}{x_2-x_1}(x_1-x_3)-y_1\;mod\;p
\]
\[
x_3=(\frac{y_2-y_1}{x_2-x_1})^2-x_1-x_2\;mod\;p\\
y_3=\frac{y_2-y_1}{x_2-x_1}(x_1-x_3)-y_1\;mod\;p
\]
相同点相加
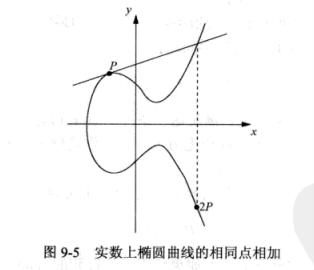 \[
x_3=(\frac{3x_1^2+a}{2y_1})^2-x_1-x_2\;mod\;p\\
y_3=\frac{3x_1^2+a}{2y_1}(x_1-x_3)-y_1\;mod\;p
\]
\[
x_3=(\frac{3x_1^2+a}{2y_1})^2-x_1-x_2\;mod\;p\\
y_3=\frac{3x_1^2+a}{2y_1}(x_1-x_3)-y_1\;mod\;p
\]
加解密
加密
B向A发送m,其中m已经被编码为椭圆曲线上的点:
- 查询A的公钥\[E_q(a,b),q,P,G,其中P=kG。k为私钥\]。
- 在\[(1,n)\]内选择随机数r(其中n为G的阶数)。
- 根据A的公钥计算\[(x_1,y_1)=rG\]。
- 计算\[(x_2,y_2)=kP\]。如果为O,则从第二步重新开始。
- 计算\[C=m+(x_2,y_2)\]。
- 将\[(x_1,y_1)和C\]发送给A
解密
\[ m=C-(x_2,y_2)=C-kP=C-rkG=C-k(x_1,y_1) \]